Carlos LópezLeiva, Kyndall Brown, and Silvia Llamas-Flores
Mathematics and daily life activities are connected. For many cultures and societies mathematics is not an isolated field or subject, it is part of an encompassing knowledge or science that helps us understand and work with the world (Cajete, 2000). Mathematics is often taught and practiced at school in ways that are rarely linked to the learners’ experiences and interests, their community, their culture, their histories, and real-life applications. However, we have learned in mathematics education that mathematics is a human endeavor (Jacobs, 1970) present across human civilizations and cultural practices such as, playing, locating, measuring, counting, explaining, and designing and building (Bishop, 1988).
Ethnomathematics is a term introduced by Ubiratàn D’Ambrosio (1991) from Brazil to describe the techniques used to explain, understand, and cope with reality in order to survive across diverse communities. Ethno relates to the members of distinct groups identified by cultural traditions, codes, symbols, myths, and specific ways of reasoning and inferring (D’Ambrosio, 1985). So, ethnomathematics refers to the way that members of various cultural groups mathematize their own reality because it examines how both mathematical ideas and practices are processed and used in daily activities (D’Ambrosio and Rosa, 2017, p. 288). In fact, this approach highlights mathematics as a cultural practice existent in human activity and challenges perspectives that present mathematics mainly as a Western—Roman, Greek—knowledge commonly taught at school. An ethnomathematical approach helps us understand mathematics from a perspective wider than traditional school mathematics, of seeing mathematics as a human act. As a result, such vision can helps renovate how we teach mathematics (Lange,1996; Rosa & D’Ambrosio, 2018).
In mathematics teaching, this approach helps us expand, affirm and redistribute mathematical authorship and empowerment; draw from and expand resources to teach and learn mathematics; recognize and challenge spaces of marginality of knowledges of many communities; and strengthen the relationship between learners and mathematics (Aguirre, Mayfield-Ingram, & Martin, 2013; Kokka, 2015). Such an approach should “perpetuate and foster—to sustain—linguistic, literate, and cultural pluralism that are part of schools” (Paris, 2012, p. 93). Thus, when students and teachers use the real world as a starting point for conceptual development, mathematics teaching and learning become more complex (De Lange, 1996) as they also become doers of mathematics (NCTM, 2000) by engaging in problem solving, multi-modal representations, and communication to develop mathematical meaning making and mathematize through their own perspectives (CCSS-M, 2010; Freudenthal, 1973).
2. What has been learned and done in ethnomathematics?
3. What can be done in the classroom?
We hope you enjoy it, and if you experience some of these or new ideas in your classroom, please share with us here, so more teachers and researchers can learn about what of ethnomathematical approaches can be implemented in the mathematics classroom.
How Is Ethnomathematics Relevant and Critical?
Ethnomathematics presents implications for classroom teachers by asking us to re-examine our beliefs and practices about what counts as legitimate mathematics, how mathematical concepts are to be taught, and how to assess children’s knowledge of mathematics. With these ideas in mind, let’s listen to a conversation between Ubiratàn D’Ambrosio and Paulo Freire as they discuss the relevance of ethnomathematics by its connection with the community thus mediating a culturally-responsive approach of teaching mathematics.
What Has Been Learned and Done in Ethnomathematics?
In the work done in ethnomathematics, we have included a selection of ethnomathematics-related works presented in three categories: (a) Mathematics community-based approaches in the U.S.; (b) Mathematics community-based approaches beyond the U.S., and (c) Ethnomathematics and critical, multicultural, culturally responsive mathematics education.
Navajo Nation Math Circles (NNMC). This is awebsite developed by NNMC designed for students and teachers of the Navajo Nation with the goal of sharing amazing mathematics activities developed by a community of mathematicians and teachers.
Mathematics and Parents as Partners (MAPPS) by Marta Civi lCivil, building on a Funds of Knowledge, develop an approach to teaching mathematics that recognizes parents as intellectual assets in the mathematical learning of their children. Through collaborations between parents (who often learned mathematics in a different way and/or in countries outside of the U.S.) and their children (often U.S.-born who are learned mathematics in U.S. schools) their different ways of understanding and doing mathematics are bridged and negotiated through communication with visual tools and hands-on materials, in a relaxed, cooperative, problem solving spaces that U.S. schools have opened for families. This process supports the transformations of negative attitudes about mathematics,the stimulation of self-confidence from learning a new skill,the learning together of mathematics in families and communities, and an excitement for mathematics through games and visual tools. Visit this site more information
Algebra Project by Bob Moses.Through experiential-based learning students engage in mathematics-related concepts activities that help them make connections to mathematics by writing about their experience in their own language and then translate their everyday language into mathematical language. For example, in the Subway Ride activity, students ride on the subway and keep track of each stop the subway makes. When the students return to the classroom, they write up their experience and make a visual representation of their trip. Teachers use their descriptions to model integer operations on the number line.
Dominoes and sports--basketball and track by Na'ilah Saud Nasir.Nasir argues that critical social, relational, and interactional dimensions should be a part of teaching and learning mathematics. Exploring out-of-school learning environments for African-American students such as: the game of dominoes, high school track-and-field, and middle and high school basketball. Nasir noticed that the participation in those settings was organized to support belonging and identification, and learning was scaffolded by expert participants. Such structures of interactions fostered respectful relationships, making mistakes acceptable, giving learners defined roles, and offering learners ways to participate that incorporate aspects of themselves.
The purchasing practice by Edd V. Taylor. Exploring purchasing competencies at local stores of low-income African-American 4- to 10-year old students, Taylor found that purchasing practices yield mathematical problem-solving opportunities. Student shopping behavior included three phases: children considered what items to purchase based upon the amount of money they had, the price of the item, and their desire for the item. In the payment phase, children brought their items to the cashier and used their money to pay for the items, recognizing coins, their values, and equivalence. In the change phase, the children received change for the overpayment of items by adding the prices of items and subtracting the total cost from the amount of money they had and made connections to bills and coins and the expected change. In each phase of the process, children engaged in meaningful mathematics.
Selling candy by Geoffrey Saxe, Terezinha Nunes-Carraher, David Carraher, & Analucía Schliemann. This group developed studies (e.g., Candy Selling and Math Learning and The Evolution of Mathematical Reasoning exploring and contrasting situated mathematical practices between school and street mathematics.
Mathematics and meaningful personal connections, community practices by Lisa Lunney Borden. Working with Mi’kmaw community in Nova Scotia, Canada, Borden highlights the importance of engaging in common learning processes between the community and school.
Matemática y simbolismo en la danza autóctona de México/Mathematics and symbolism of traditional Mexican dances by Everardo Lara González (in Spanish). González presents links between community practices, such as Anahuac dance and symbols with intuitive mathematics embedded in the rhythm.
Current and Future Perspectives of Ethnomathematics as a Program by Milton Rosa and Ubiratàn D’Ambrosio. Understanding ethnomathematics as a way to act in the world, Rosa and D’Ambrosio with other authors describe different ways of doing mathematics (e.g., procedures, concepts, processes, methods, and practices) by considering the appropriation of academic mathematical knowledge developed by different sectors of the society as well as by considering different modes in which different cultures negotiate their mathematical practices.
Ethnomathematics: Challenging Eurocentrism in Mathematics Education by Arthur B. Powell, Marilyn Frankenstein.
Relearning Mathematics: A Different Third R - Radical Maths by Marilyn Frankenstein.
Culturally Responsive Mathematics Education by Brian Greer, Swapna Mukhopadhyay, Arthur B. Powell, Sharon Nelson-Barber.
Critical Mathematics Education and An Invitation to Critical Mathematics Education by Ole Skovsmose.
Cognition in Practice by Jean Lave.
What Can Be Done in the Classroom?
In this section, we present some examples of ethnomathematics activities that could be implemented in the classroom. In the first group, we provide three general topics and ideas. In the second group of resources, we provide a list of books and programs that include already developed activities that can be implemented in the classroom. Finally, the last group are online resources with ideas and materials that could be utilized in the classroom.
Mayan number system. The Mayan/Mesoamerican numeral system was used to represent calendar dates. It is a vigesimal (base-20) numeral system. The numerals include three symbols; zero (shell), one (dots or stones) and five (a bar or stick).
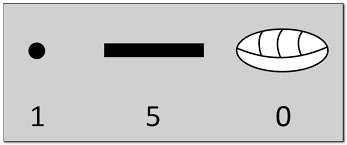
TheYoruba number system. The Yoruba people live in Nigeria. The Yoruba number system is a vigesimal (base 20) system and it relies on subtraction. For example, numbers 11, 12, 13 ,14 are understood as ten plus one, plus two, etc.; but from 15 to 19 these numbers are understood as 20 minus five, four, etc. Likewise, after 20, from 21-24 is 20 plus ‘x’, and from 25-29 is 30 minus five, four, and so on. Then higher numbers are identified with multiples of 20, Ogoji, two twenties (40), Ogota, three twenties (60), Ogorin, four twenties (80). Ogorun, five twenties (100), and so on to ten twenties (200), when the word Igba is used.
African fractals. A fractal represents fragmented geometric shapes that can be subdivided into parts, each of which is a reduced-size copy of the whole. The five Essential Components of Fractal Geometry are
Fractional Dimension-The theory of measurement that governs fractals allows dimensions to be fractions.
Fractals are present in nature and many cultures. For example, in African villages, fractals are embedded in the architecture, textiles, art and religion. An example of an African Fractal includes the Lusona Sand Drawings, created by Chokwe people in Angola. These sand drawings are called Sona. These drawings are used both in their decorative artwork and in their story-telling tradition. There are 5 Rules for these drawings: (a) Do not connect the dots. Lusona lines go around and between the dots, but never touch them; (b) you can begin your first line between any two dots on the array; (c) once a starting point is decided, draw a straight line at 45 degrees between the dots. When you reach the edge of the array, turn your line 90 degrees and make another straight line; (d) you may cross a line that you’ve already made, but don’t trace over the same line twice; (e) If the end of the line meets it’s own beginning, that’s a closed line. Once you’ve made a closed line, you may need to find another place in the array to begin another line. Use a different color for each closed line to help you see the patterns more closely. Go to this link for additional information.
Annual Perspectives in Mathematics Education (APME). APME presents work of teachers, school counselors and administrators, teacher educators, and education researchers to promote a mathematics teaching and learning that is humane, positive, and powerful for students who are Black, Indigenous, and/or Latinx. The book sections include: Attending to Students’ Identities through Learning, Professional Development That Embraces Community, and Principles for Teaching and Teacher Identity.
Math Is a Verb: Activities and Lessons from Cultures Around the World by Jim Barta, Ron Eglash, Cathy Barkley. This book provides guides for teachers who want to integrate mathematics instruction with activities from different cultures. Activities are culturally situated and linked to Common Core objectives.
Mathematics of the Americas by TODOS: Mathematics for ALL—Barta, Llamas-Flores, & Galima (2009). This booklet presents four classroom activities for each of the grade bands K-3, 4-8, and 9-12 related to Navajo, Inca, Maya, and Aztec cultures and mathematics.
TEACH Math. Teachers Empowered to Advance Change in Mathematics (TEACH Math) Project's primary goal is to suggest processes and activities that support prospective and early career teachers in developing the knowledge, beliefs, dispositions, and practices needed to effectively plan, adapt and implement mathematics instruction in culturally, linguistically, and socio-economically diverse schools.
Examples of ethnomathematics in action. This site describes mathematics included in different cultures, music, and sports.
Integrating Mathematics of Worldwide Cultures into K-12 Instruction by Terry Herrera and Judy Spicer. is a list of resources to teach mathematics through multicultural approaches. Presented at the 2011 National Council of Supervisors of Mathematics (NCSM) Conference in Philadelphia.
Google site, lesson plans on ethnomathematics. Access diverse lessons and materials related to ethnomathematics.
Lotería and mathematics by Olga Ramírez and Cherie McCollough. Learn how Lotería can support the learning of mathematics with families.
Ethnomathematics approach to teaching language minority students by David M. Davison. The article presents prescriptions on how ethnomathematics support learning of culturally diverse learners.
The importance of ethnomathematics in the math class by Alex Brandt and Egan J Chernoff. This manuscript presents ideas on integrating ethnomathematics in school mathematics teaching.
Linking mathematics and culture to teach geometry concepts by Vincent Snipes and Pamela Moses. This manuscript presents ways of implementing the task: “Finding the Center of a Rectangular Box Top” to support ethnomathematical approaches in the classroom.
References

